はじめに
今回は、「ゼロから作るDeep Learning」という本を読んで、なぜ数値微分で勾配を求めるより誤差逆伝播法の方が早いのかやっと理由がわかったのでまとめてみます。
なかなかなぜ早いのか、という記事がなかったのですが、皆さんすんなり理解されてるからですよね。自分は引っかかってしまったので、自分なりにまとめてみます。
※要は、数値微分の計算方法について理解できていなかった
本記事の対象者
- 数値微分について理解が曖昧な人
- なぜ誤差逆伝播法が数値微分より早いのかわからない人
- 初学者
- 誤差逆伝播法について大体理解できている人
- ゼロから作るDeep Learningを読んで大体わかった人
※注意
- 筆者はまだ初学者なので間違っている部分を含む可能性があります。その際はコメント欄で教えていただけると助かります。
- 「完全に理解した」とか言ってますが、説明は完璧ではありません。随時改良していきますのでコメント欄でアドバイスよろしくお願いします。
まず数値微分について理解する
数値微分の式(前方差分)
$$
\lim_{h \to0}
\frac{f(x+h)-f(x)}{h}
$$
数値微分の式(中心差分)←傾きの誤差が少ないので今回はこれを使用する
$$
\lim_{h \to0}
\frac{f(x+h)-f(x-h)}{2h}
$$
limitでhを0に極限まで近づけて計算すると微分が求まります。普通は極限まで近づけたhを0として計算しますが(これを解析的な微分と呼ぶ)、コンピューターに0を代入した計算式を入れるとエラーが起きるので、実際には「0に近い数字」を使います。
(分母に0が入ったら、エラーを起こしますよね。具体的には1/0をしてるようなものです)
なので、解析的な微分の値と誤差が出てしまいますが、それはしょうがないので無視していきましょう。
def numerical_diff(f, x):
h = 1e-4 #0に近い値
return (f(x+h) - f(x-h)) / (2*h)Pythonで書くとこんな感じになります。引数のfが計算する関数、xが計算する関数の引数です。
二乗和の関数を偏微分する
$$
f(x)=x^2+y^2
$$
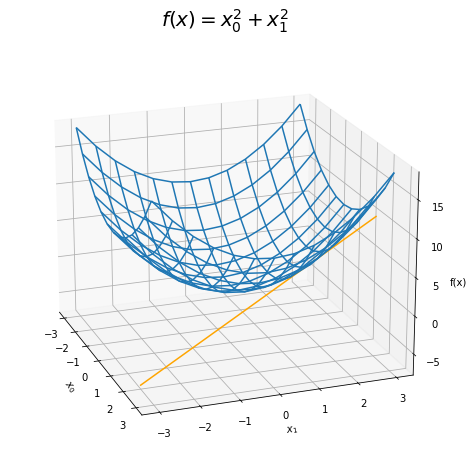
\( x_0 \)はx、\( x_1 \)はyと見てください
xについて偏微分
$$
\frac{\partial f}{\partial x} = 2x
$$
yについて偏微分
$$
\frac{\partial f}{\partial y} = 2y
$$
Pythonでxについて偏微分してみる
# xを固定した二乗和の関数
def f(x):
#yの値を固定
y=2.0
# 二乗和を計算
return x**2 + y**2
Pythonでyについて偏微分してみる
# xを固定した二乗和の関数
def f(y):
#xの値を固定
x=2.0
# 二乗和を計算
return x**2 + y**2
つまりは、xかyどちらかを固定して(具体的な数値を入れて)数値微分すれば偏微分ができる。
単純なニューラルネットワークの勾配を求めてみる
$$
W=\begin{pmatrix}
w_{1} & w_{3} & w_{5} \\
w_{2} & w_{4} & w_{6}
\end{pmatrix}
$$
$$ \frac{\partial E}{\partial W}
=\begin{pmatrix}
\frac{\partial E}{\partial w_{1}} & \frac{\partial E}{\partial w_{3}} & \frac{\partial E}{\partial w_{5}} \\
\frac{\partial E}{\partial w_{2}} & \frac{\partial E}{\partial w_{4}} & \frac{\partial E}{\partial w_{6}}
\end{pmatrix}
$$
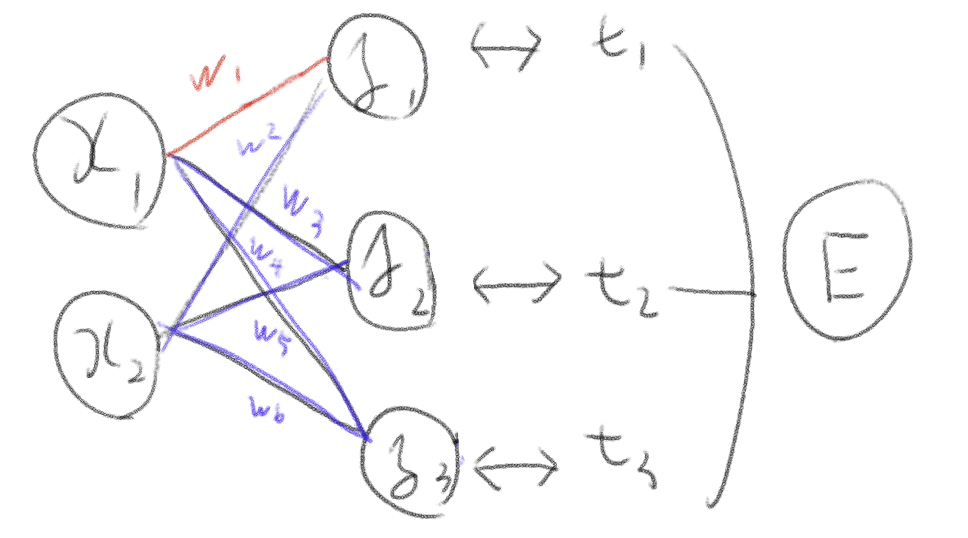
この簡単な式に騙されてしまった。実際は関数の偏微分をした時と同様、E(Loss)を求めるために他のバイアスや重みを固定して計算する必要がある。
(赤の部分の勾配を求めるのに、赤+青+活性化関数などの部分も計算しなくてはならない)
なので、数値微分(中心差分の場合)だと、
- 特定のWの重みを+0.00001(0に近い値)して、それ以外のパラメーターやバイアスを固定してニューラルネットワーク全体を計算する
- 計算した結果の誤差関数の値を記録
- 特定のWの重みを-0.00001(0に近い値)して、それ以外のパラメーターやバイアスを固定してニューラルネットワーク全体を計算する
- 計算した結果の誤差関数の値を記録
- それらを中心差分で求める
太文字がとにかく処理が遅い!!なんてったって、ある特定の重みを変えた時、それに関係しないバイアスや重みの値を全て固定してニューラルネットワーク全体の推論処理をして勾配を求めないといけないから。
少し層が増えると計算量はさらに増える
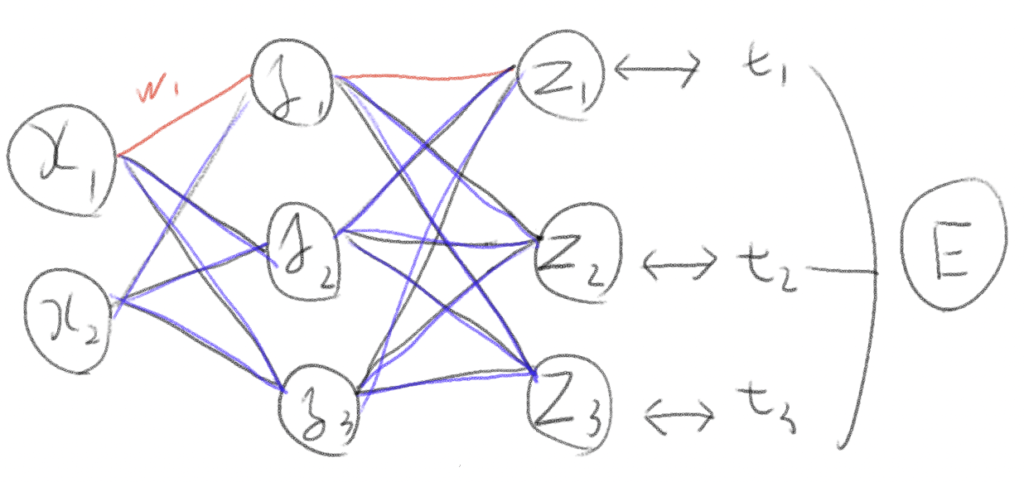
数値微分でW1の勾配を求めようとすると、赤い部分+紫の部分+活性化関数などを全て計算しなくてはならない。
全体を計算する=各重みの積→各重みの積の和→それらを活性関数に通すの繰り返し!!
それに比べ誤差逆伝播法は
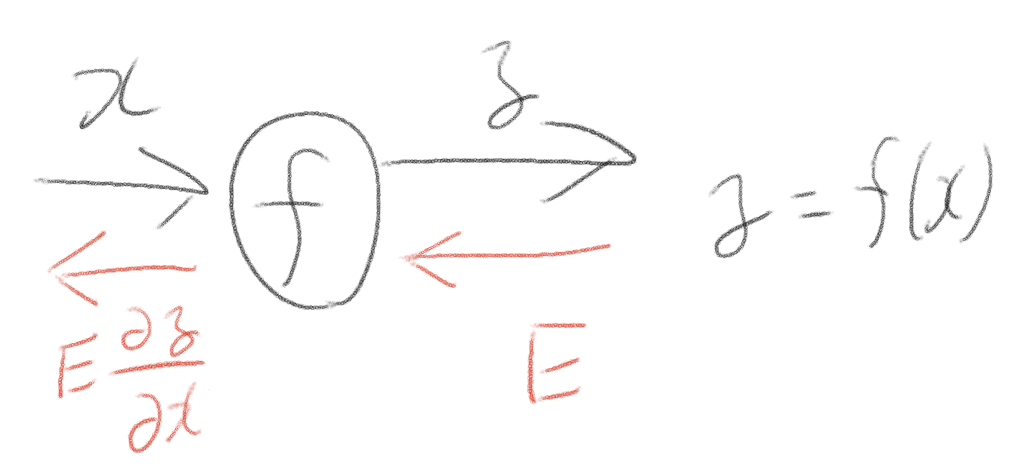
基本的な仕組み。Eというロスを連鎖律を使って後ろに伝播していく。
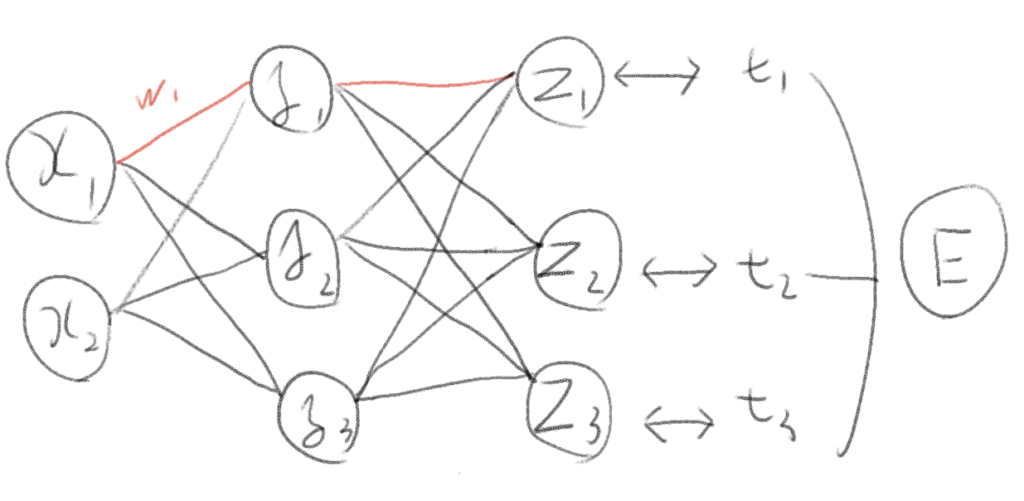
W1の重みの勾配を求めようとした時、赤い部分だけを連鎖律を使って計算すれば良い。
まとめ
- 数値微分はパラメーター一つに対してニューラルネットワーク全体を計算しないといけないため非常に計算量が多い
- それに比べ誤差逆伝播法はパラメーターに関する部分だけを偏微分していって、その微分の値を後ろに伝え、目標のパラメーターの勾配を計算できる
- しかも誤差逆伝播法は、一度計算した偏微分の値を保存しておき、他のパラメーターが参照することによって計算の重複を防ぐことができる!
最後に
めちゃくちゃ雑に書いてしまいましたが、随時わかりやすく情報を追加したり改良したりしていくので、よろしくお願いします。
わからないところなどがあったらコメントしてもらえると、さらに記事を改良できるので、ぜひコメントよろしくお願いします!
記事のSNSシェア、共有よろしくお願いします!
他にも記事を書いているので、ぜひご覧ください!


参考にさせていただいたサイト

めちゃくちゃに誤差逆伝播法の計算方法がわかりやすかった。
ゼロから作るDeep Learningを読んでいる人にはうってつけの記事。本に書いていないことや、書いているものを噛み砕いていたりする。(シリーズなので、勾配以外の記事も書いてある)







コメント